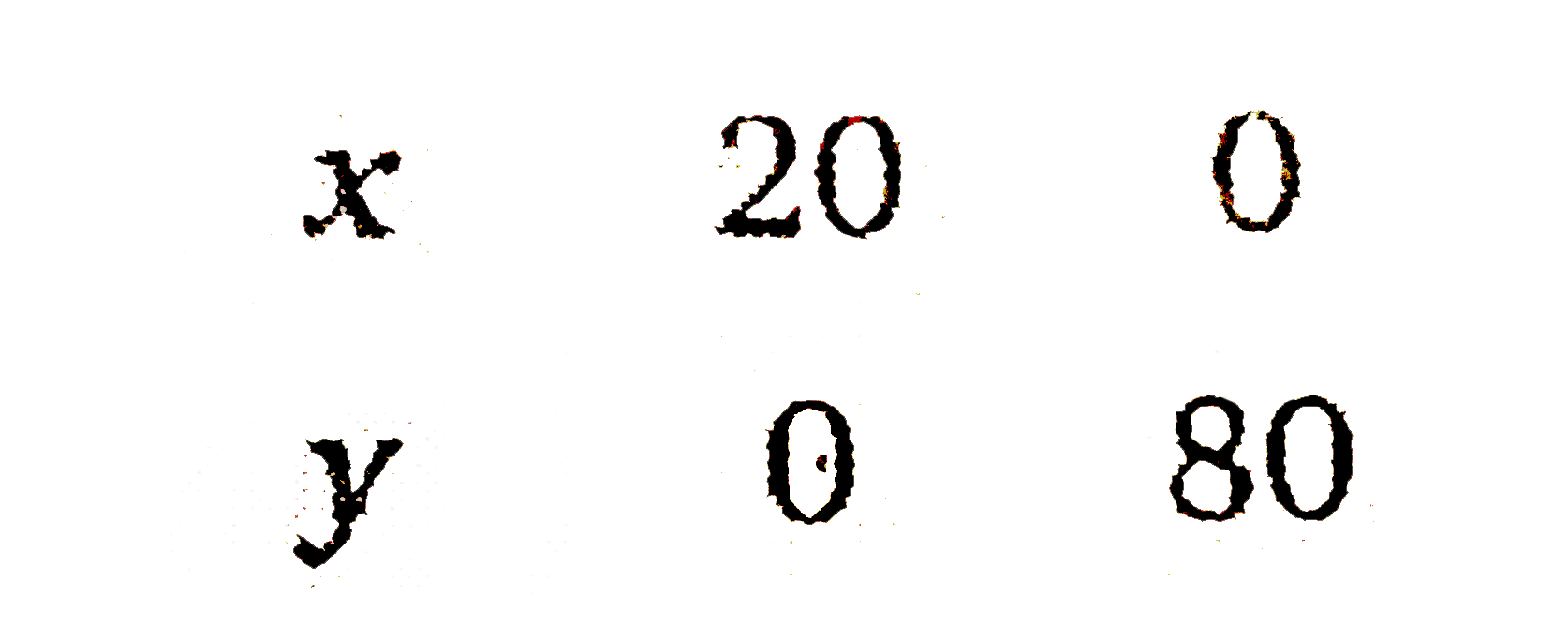If X 12y And X 6y 90 Then X
If X 12y And X 6y 90: An Analysis of the Relationship Between Variables
In mathematics, equations are used to explore the relationships between variables. One such equation is the equation “If X 12y And X 6y 90”. This equation has two variables, X and y, that can be used to determine the value of one, based on the value of the other. In this article, we will explore the relationship between the two variables in order to understand the equation and its implications.
h2: Understanding the Equation
The equation “If X 12y And X 6y 90” is a linear relationship between the two variables, X and y. This means that when one variable changes, the other variable changes in the same proportion. In other words, if we double the value of X, then the value of y should also double. Similarly, if we halve the value of X, then the value of y should also halve.
h3: Exploring the Implications of the Equation
The equation “If X 12y And X 6y 90” allows us to analyze the relationship between the two variables, X and y. For example, if we can determine the value of one variable, then we can use the equation to determine the value of the other. This can be applied to many different situations, such as solving for the unknown in a system of equations or finding the slope of a line.
h4: Utilizing the Equation
The equation “If X 12y And X 6y 90” can be used to solve a variety of problems. For example, if we are given three numbers, we can use the equation to determine the fourth number. Additionally, the equation can be used to determine the slope of a line, or the rate at which one variable changes as the other changes.
Conclusion
The equation “If X 12y And X 6y 90” is a linear relationship between the two variables, X and y. This equation can be used to determine the value of one variable based on the value of the other. Additionally, this equation can be used to solve a variety of problems, such as finding the fourth number in a set of three or determining the slope of a line. By analyzing the equation and its implications, we can gain a better understanding of how the two variables interact.
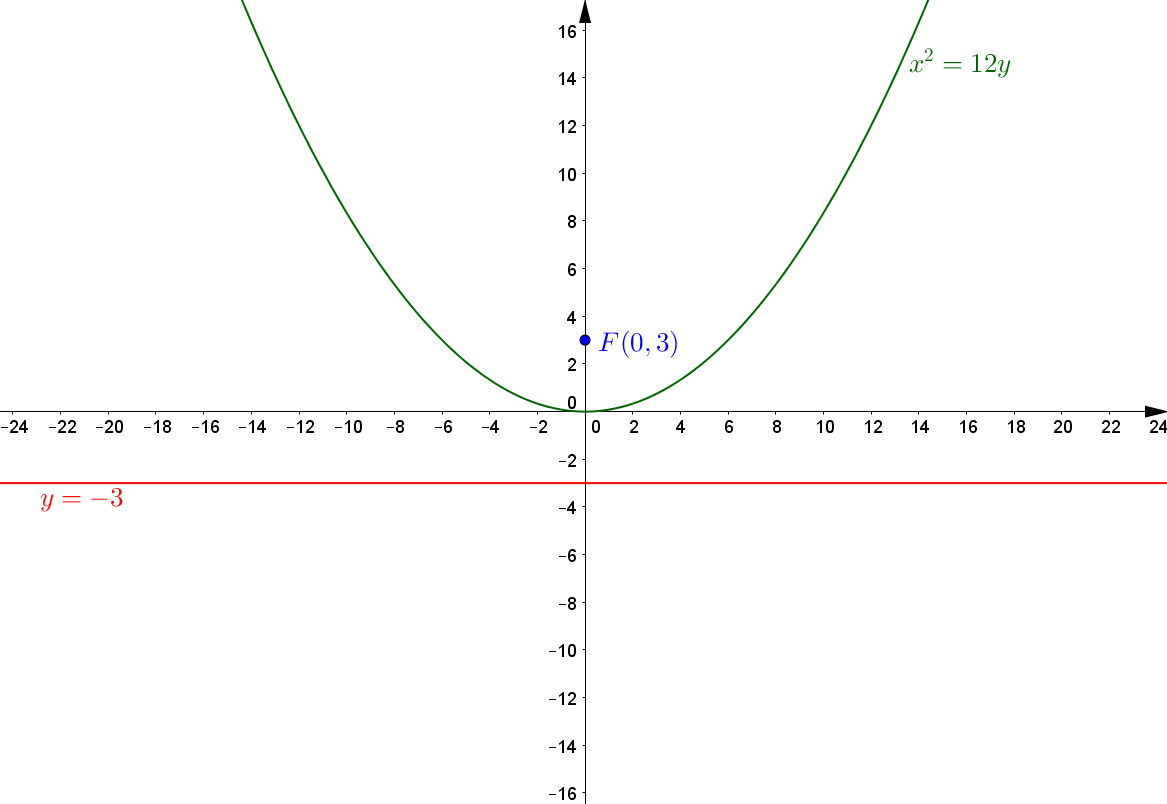
`x^2=12y` Graph the equation. Identify the focus, directrix, and axis
If 3x - 5y = 1, 2x/x-y= 4, then the value of (x + y) is :(a) 3(6) - 3c

(Diet problem) A dietician has to develop a special diet using two