Factor Out The Greatest Common Factor From The Polynomial
Polynomials are mathematical expressions composed of a combination of variables and constants. They can be used to represent functions, equations, and relationships between various elements. A great common factor (GCF) is the largest number that is a factor of two or more numbers. Factorizing polynomials involves breaking them down into their factors, so that they can be simplified. Finding the greatest common factor of a polynomial is an important step in factorizing and simplifying it.
What is a Greatest Common Factor?
A greatest common factor (GCF) is the largest number that is a factor of two or more numbers. It is also known as the greatest common divisor (GCD). Factors are numbers that can be multiplied together to produce a given number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The greatest common factor of 12 is 12.
How to Factor Out the GCF from a Polynomial?
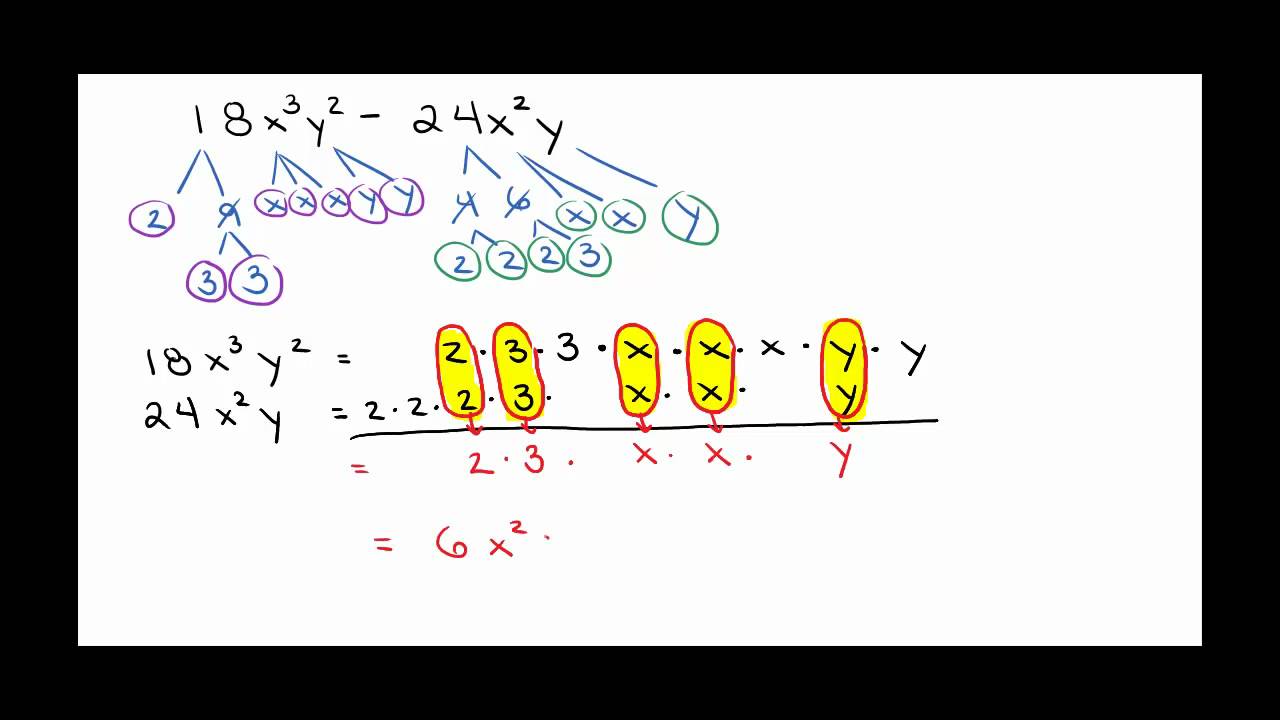
Factoring out the greatest common factor from a polynomial is a process of breaking the polynomial down into its factors and then finding the largest factor that is common to all of them. This can be done by grouping the terms of the polynomial together and looking for common factors.
For example, consider the polynomial 3x2 + 6x + 9. The first step is to group the terms together. This can be done by writing the polynomial in the form (3x2 + 6x) + 9. The next step is to look for any common factors. In this case, the common factor is 3, which is the greatest common factor.
Factoring Out the GCF
Once the greatest common factor has been identified, it can be factored out. This is done by dividing each term of the polynomial by the greatest common factor. In the example above, each term is divided by 3. The resulting polynomial is x2 + 2x + 3. This is the polynomial with the greatest common factor factored out.
Simplifying the Polynomial
Factoring out the greatest common factor is a useful method for simplifying polynomials. This is because it reduces the number of terms in the polynomial. In the example above, the polynomial was simplified from three terms to three terms.
Using the GCF to Solve Equations
The greatest common factor can also be used to solve equations. This is done by factoring out the GCF and then using the same factor to solve the equation. For example, consider the equation 3x2 + 6x + 9 = 0. By factoring out the GCF, the equation can be simplified to x2 + 2x + 3 = 0. This equation can then be solved by using the factorization method.
Conclusion
Finding the greatest common factor of a polynomial is an important step in factorizing and simplifying it. Factoring out the greatest common factor can reduce the number of terms in the polynomial and make it easier to solve equations. It is a useful tool for simplifying polynomials and equations.
Factoring Polynomials Part 1: Factoring out the GCF (Greatest Common
Greatest Common Monomial Factor - slidesharetrick

Solving Equations By Clearing Fractions - Lessons - Tes Teach
